The trefoil image
within the cover
designed by Ben Laurie
IDEAL
KNOTS - WHAT ARE THEY?
From the topological point of view the conformation of a knot is of no importance. For a physicist such a conformational invariance takes place when a knot is tied on a perfect thread i.e. an infinitely thin and perfectly flexible filament whose interaction with itself is limited only to hard repulsion at the points of the self-contacts. In such a case, the length of the thread on which the knot is tied is also irrelevant. However, when a knot is tied on a perfect rope, i.e. perfectly flexible filament of a circular cross-section, whose diameter is finite and fixed, its length matters a lot: simply, if the rope is too short, the knot may happen to be too complex to be tied on it. A natural question arises: which is the conformation of the knot which needs for its tying the shortest piece of the perfect rope? Conformations, which minimize the length of knots tied on the perfect rope are called ideal.
For the first time the word "ideal" was used by J. Simon. The term was used
in the context of any given energy function. The term "ideal knots"
has been coined by Andrzej
Stasiak [1]. An ideal knot is a knot tied with a shortest possible piece
of a perfect rope. A perpendicular cross-section of a perfect rope makes
always a circle of a fixed diameter D. Thus, the perfect rope is perfectly
hard - you cannot squeeze it. At the same time, however, the perfect rope
is perfectly flexible - you may bent it without any effort. The radius R
of the bending is limited of course by the fixed diameter D: R
cannot be smaller than D/2. First results of the extensive numerical
search carried out by the Lausanne group for the ideal knots were presented
in Ref. [1] and [2].
Various modifications of the problem of ideal knots have been considered independently
by a number of scientists, mostly mathematicians. The present state of art
in this field is presented in Ref. [3], where you will find papers by L. Kauffman, H. K. Moffat,
Jun O'Hara, E. J. Janse van Rensburg
and his coworkers, Eric Rawdon,
J. Calvo, Y.
Diao, A. Yu. Grosberg, R. B.
Kusner & J. M. Sullivan,
Ben Laurie and others.
[1]
V. Katritch, J. Bednar,
D. Michoud, R.
G. Scherein, J. Dubochet
and A. Stasiak, Geometry and physics of knots , Nature 384 ,
142 (1996).
[2] V. Katritch, W.K. Olson, P. Pieranski,
J. Dubochet and A. Stasiak, Properties of ideal composite knots, Nature
388, 148
(1997).
[3] "Ideal
Knots" , eds. A. Stasiak, V. Katritch and L. H. Kauffman, World Scientific
1998.
The trefoil image
within the cover
designed by Ben Laurie
THE SONO ALGORITHM
Finding the ideal conformation of a knot is not an easy task. Working on the problem I developed SONO (ShrinkOnNoOverlaps)- a simple but very fast algorithm which takes the initial conformation of a knot and simulates a mechanical process in which the rope, on which the knot was tied, shrinks in small steps while its diameter is kept constant [4,5]. During the process the knot is forced to change its conformation until no further shrinking is possible. Figure below shows how the process runs in the case of the trefoil knot.
The price paid for the simplicity of the SONO algorithm is its inability to get out of the local minima (unless the minima are shallow) within which conformations of many knots easily get stacked. The phenomenon is of vital importance in the case of composite knots. To test the SONO algorithm I performed a series of tests. Below I briefly describe them.
[4]
P. Pieranski, Searching for ideal knots , Pro Dialog, 5, 111 (1996).
(in Polish)
[5] P.
Pieranski, In search of ideal knots , in "Ideal Knots" , eds.
A. Stasiak, V. Katritch and L. H. Kauffman, World Scientific 1998.
UNTANGLING THE UNKNOT
Take an unknot, entangle it in an arbitrary manner and fetch the conformation to the input of the SONO algorithm. SONO will disentangle it in a reasonable time finishing with a circle - the unquestionable ideal conformation of the unknot. Figure below presents consecutive stages of such an untangling process.
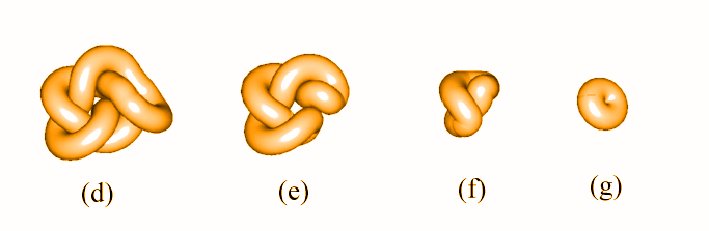
CONJECTURE.
There is not such a conformation of the unknot that could not be disentangled
by the SONO algorithm.
REMARK.
I formulated the conjecture at the beginning of my work with SONO (the end
of 1998). Today (the beginning of 2002) I know, that the conjecture
is wrong. Stimulated by Andrzej Stasiak, I have found such a conformation
of the unknot, which cannot be untangled by SONO. It cannot be untagled by
anything or anybody without cutting the rope. It's a Gordian conformation. There are infinitely
many of them.
MOFFAT TEST
Another test of knot tightening algorithms was suggested by Moffat. As he put it in his comment [6] to Ref. [1]: "It would be interesting to test the algorithm on the simpler T 3,2 and T 2,3 configurations of the trefoil; it is not clear to me, how T 3,2 could flow to T 2,3 through the process described." The task defined by Moffat is not easy to perform. Parametrically defined torus knots T 3,2 and T 2,3 are of different symmetry. To get into the ideal final conformation the tightening algorithm should be able to break the symmetry of the initial conformation. Figure below presents how the SONO algorithm deals with this problem.
[6]
H. K. Moffat, Pulling the knot tight , Nature, 384, 114 (1996).

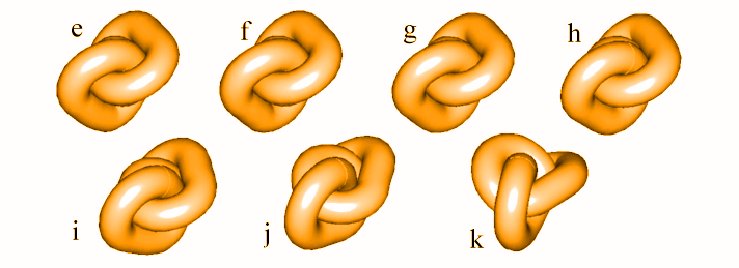
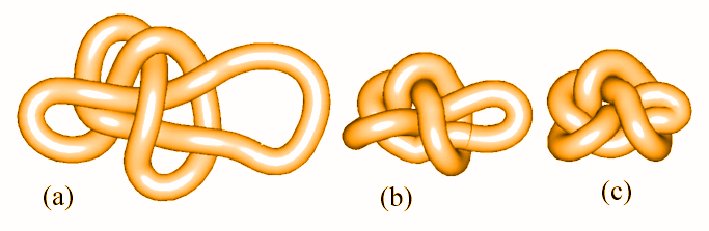
PERKO PAIR TEST
Another test, which any algorithm aimed at finding the ideal conformations of prime knots should pass is the ability to bring knots 10 161 and 10 162 , the Perko pair, to a single, ideal conformation. Below we present how the is performed by the SONO algorithm. Initial conformations (a) of the Perko pair knots were defined by redrawing on the screen the conformations found in „The Knot Book" by C. C. Adams, p.32. The conformations were tightened separately with the SONO algorithm. Figure below shows consecutive stages of the knots evolution. As checked by an additional knot comparing procedure, although differently oriented, the final conformations of the knots are identical.
Knots on the Web - the most complete (according to me) set of links to the www knot pages is maintained by Peter Suber, Department of Philosophy, Earlham College, Richmond, Indiana, 47374, U.S.A. Do not waste time using any search engines, just have a look there!