THE BOUNCING BALL MODEL
It is one of the cheapest and the most
prolific
experimental systems I made. It is probably the simplest experimental
system
in which the period doubling route to chaos has been observed.
From the theoretical point of view the
bouncing
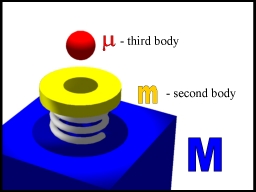
ball model - a system in which a ball bounces on a vibrating surface -
can be seen either as a particular three body system or as a system of
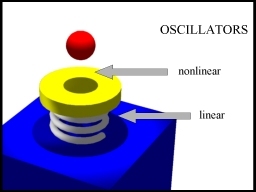
two coupled oscillators. One of the oscillators, (m, M) is linear. The
other one, (m,
M), is strongly non-linear.
To make the experiment you need:
1. a steel ball of diameter around 4
mm
2. a glass or plastic concave lens
3. a loudspeaker
4. an audio frequency generator
Attach the loudspeaker to the table so that its
membrane
is oriented horizontally.
Attach the lens to the membrane of the
loudspeaker.
(Make sure the lens stays far enough from the loudspeaker magnet.)
Connect the loudspeaker to the generator and
make the lens vibrate with a frequency about 60 Hz.
Drop the ball onto the surface of the vibrating
lens.
Adjust the amplitude of the surface vibration
so that the ball starts bouncing on it.
Observe (and listen to) the changing
modes
of the ball bouncing motion at the increasing amplitude of the surface
vibrations.
Experiments that we performed allowed us to record a number of
essential phenomena observed in the nonlinear systems.
To record the phenomena we were recording the phase of the consecutive
collisions of the bouncing ball with the oscillating surface.
In the experiments the amplitude of the surface vibration was swept
either up or down.
Here is list of the basic observations we made:
1. Their period-doubling routes to
chaos.
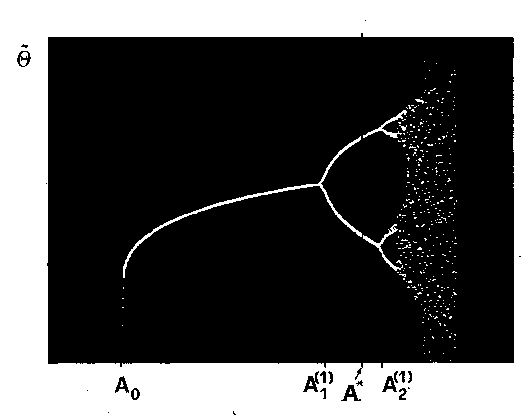
The picture below presents the bifurcation diagram of the BB system
recorded in the experiment where the amplitude A of the surface
vibrations was swept down. The
bifircation diagram recorded in the experiment contains the simplest
periodic mode and its period-doubled versions.
Here is the most interesting part of the diagram:
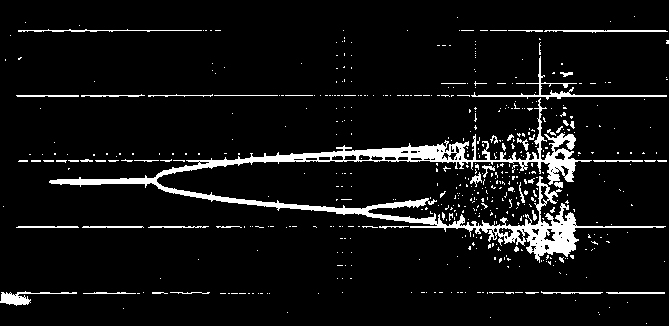
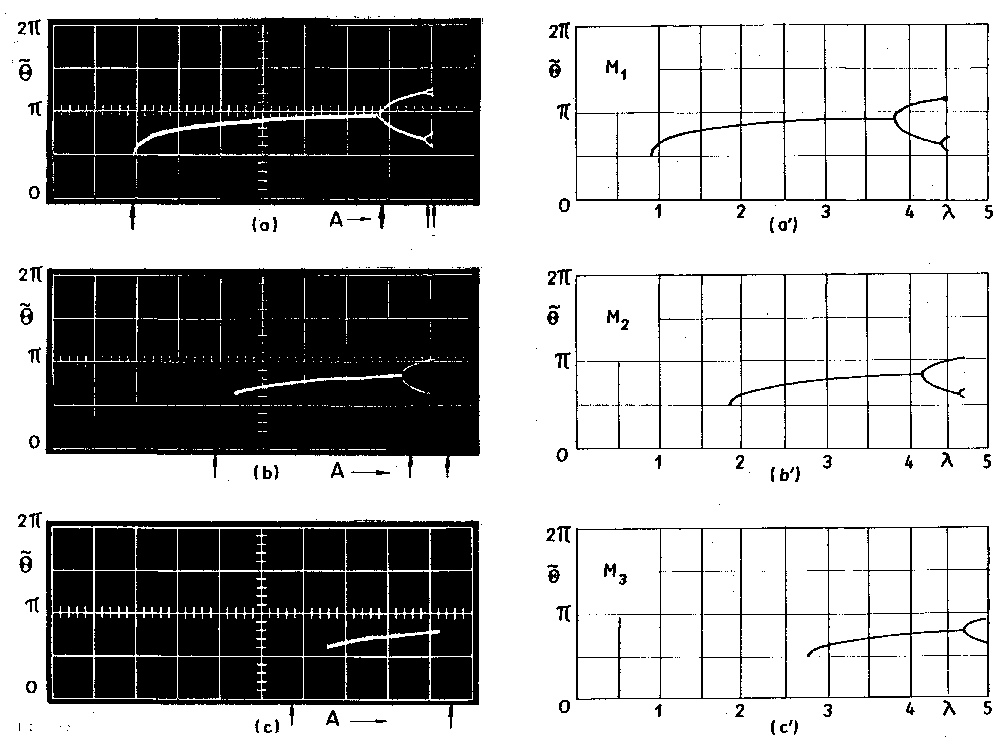
One of the most characteristic features of the nonlinear dynamical
systems is that at the same value of the control parameter, here - the
amplitude of the surface vibrations, the system may stay in a few
coexisting vibration modes. The picture below (left) presents the
bifurcation diagram of three of them denoted as M_1, M_2 and M_3. The
diagrams presented on the right were obtained from numerical
simulations of the laboratory experiments.
As we have found, apart from the simple periodic modes and their
period-doubled variations it is possible to observe also their
period-trippled versions. The picture below provides an experimental
evidence.
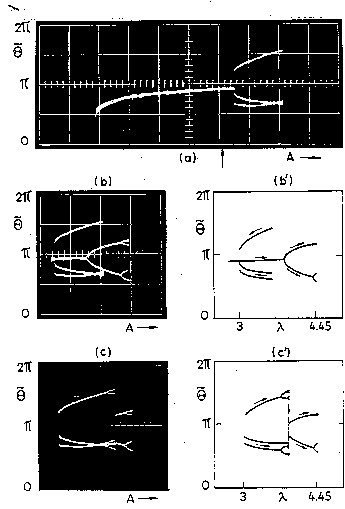
All of the presented above modes of motion are described in detail in: P. Pieranski, Z. Kowalik and M. Franaszek, Jumping particle model. A study of the
phase space of a nonlinear dynamical system below its transition to
chaos. J. Phys. (Paris), 46,
681 (1985).
2. Critical slowing down and
hysteresis around the bifurcation points.
The dynamics of the phase oscillations suffers a critical slowing down
near the bifurcation points. Thus, moving up and down through the
bifurcation diagrams at a finite rate causes inevitably hysteresis
effects. The picture below presents the experimental evidence for the
phenomenon and its numerical simulation:
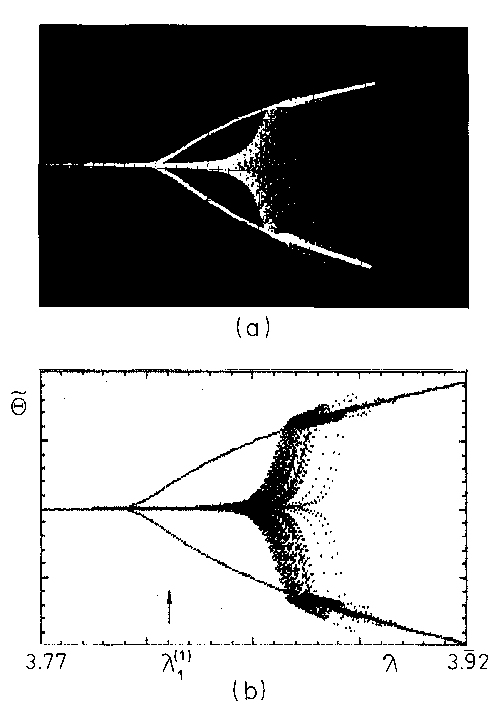
Notice the assymetry of the hysteresis effects. There is a large
dispersion in sweeps up, while in sweeps down it is hardly visible. The
phenomenon was explained in: P. Pieranski
and J. Malecki, Noise-sensitive
hysteresis loops around
period-doubling
bifurcation points. Nuovo Cim. 9,
757 (1987).
3. Resonances
of the basic periodic modes.
Observing, at a given value A of the surface vibration amplitude, the
phase of the consecutive collisions one finds that is behaves as a
damped harmonic oscillator. Its resonant frequency depends on A. The
frequency is thus different at different parts of the bifurcation
diagram. The picture below presents the bifurcation diagrams recorded
in presence of a periodic perturbation of various fixed
frequencies. Plots shown on the right were obtained from numerical
simulations.
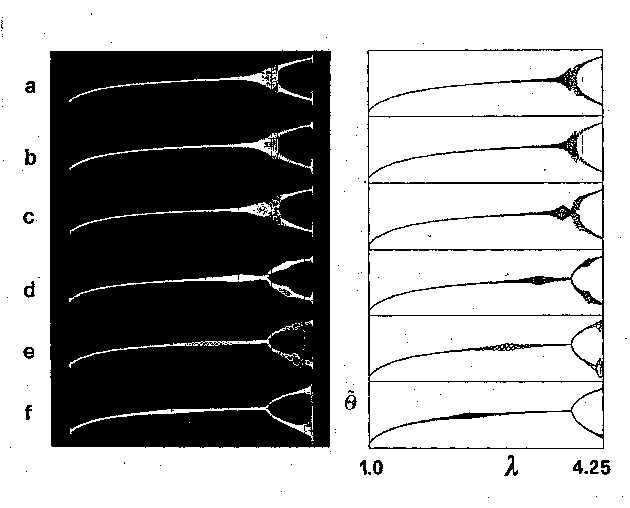
As seen in reordings (a), (b) and (c)
above, where the frequency of the periodic perturbation was close to
the half of the frequency of the surface vibration, the bifurcation was
suppressed. Pictures below show this in more detail.

Details of the experiments are described
in P. Pieranski and J. Malecki, Noisy precursors and resonant properties of
the period, doubling modes in a nonlinear dynamical system. Phys. Rev. A 34, 582 (1986).
----------------
A virtual version of the experimental system
is
described in: Bouncing
Ball Workbench.
Its DOS Pascal implementation is zipped together
with a few other files needed to run it in: BBW
 A high quality bouncing
ball experimental set-up has been designed by Brad
E. Paden.
A high quality bouncing
ball experimental set-up has been designed by Brad
E. Paden.
A threepenny experiment on the ball
bouncing on the motionless surface has been performed and carefully
analysed by Éric Falcon & Stéphan Fauve.
Publishes papers
P. Pieranski
Jumping particle model. Period doubling
cascade in an experimental system.
J. Phys. (Paris), 44, 573 (1983).
P. Pieranski, Z. Kowalik and M. Franaszek,
Jumping particle model. A study of the
phase space of a nonlinear dynamical system below its transition to
chaos.
J. Phys. (Paris), 46, 681 (1985).
P. Pieranski and R. Bartolino,
Jumping particle model. Modulation modes
and resonant response to a periodic perturbation.
J. Phys. (Paris), 46, 687 (1985).
M. Franaszek and P. Pieranski,
Jumping particle model. Critical slowing
down near the bifurcation points.
Can. J. Phys. 63, 488 (1985).
P. Pieranski and J. Malecki,
Noisy precursors and resonant properties of
the period, doubling modes in a nonlinear dynamical system.
Phys. Rev. A 34, 582 (1986).
P. Pieranski and J. Malecki,
Noise-sensitive hysteresis loops around
period-doubling
bifurcation points.
Nuovo Cim. 9, 757 (1987).
P. Pieranski,
Direct evidence for the suppression of period
doubling , in the bouncing ball model.
Phys. Rev. A 37, 1782 (1988).
Z. Kowalik, M. Franaszek and P.
Pieranski,
Self-reanimating chaos in the bouncing ball
system.
Phys. Rev. A 37, 4016 (1988).








 A high quality bouncing
ball experimental set-up has been designed by Brad
E. Paden.
A high quality bouncing
ball experimental set-up has been designed by Brad
E. Paden.